Linear Regression with PyTorch: The Essential Beginner's Guide

1. Introduction

Linear Regression with PyTorch is one of the most practical and beginner-friendly ways to understand predictive modeling in machine learning.

Have you ever wondered how analysts and businesses predict future prices, like houses, stocks, or even your monthly electricity bill?

Linear regression, one of the foundational techniques in machine learning, makes these predictions straightforward and interpretable.

This comprehensive guide takes you step-by-step through linear regression using PyTorch, perfect for both beginners and intermediate learners.

2. Understanding Linear Regression

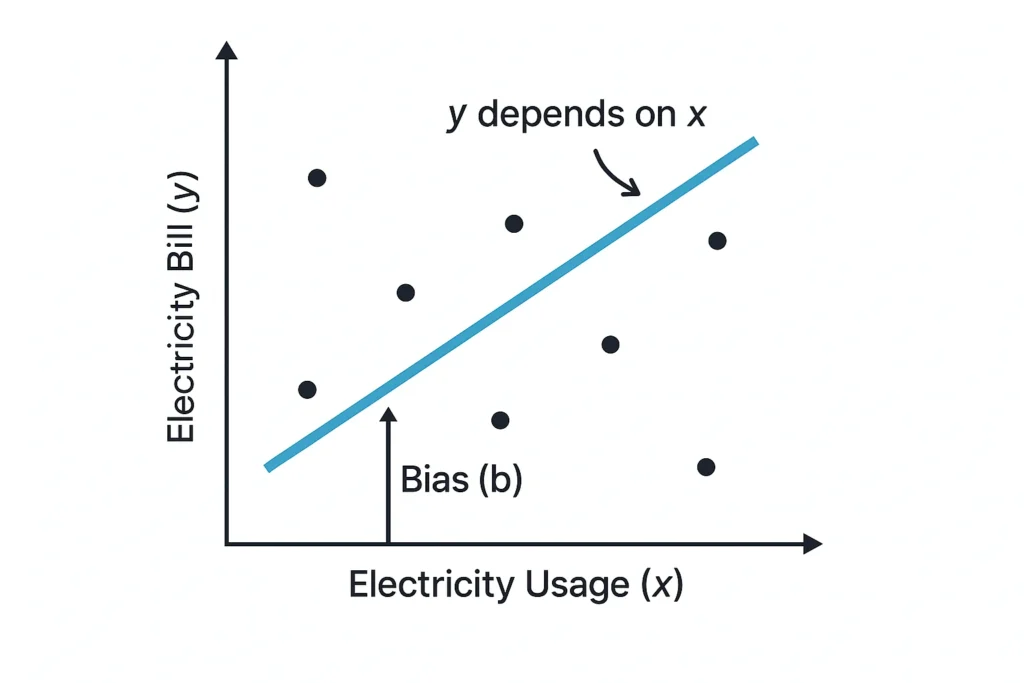
Linear Regression with PyTorch identifies and quantifies the relationship between two variables by fitting a straight line. For example, predicting your electricity bill based on your monthly usage.

This relationship is expressed as:

\begin{matrix} y = w x + b \end{matrix}

Where:

y: Predicted electricity bill (dependent variable) – it depends on how much electricity you use
x: Electricity usage (independent variable) – it’s the input that you control or measure
w: Slope — how much the bill increases per unit of electricity
b: Bias — fixed monthly fee regardless of usage

Think of it like this: the more you drive, the more fuel you use. Fuel usage (y) depends on how far you drive (x). That’s exactly how dependent and independent variables work.

The graph below visually explains how electricity usage influences your bill. It shows a straight line representing the predicted relationship between input (usage) and output (bill), just as described in the equation y = wx + b.

3. Making Predictions with PyTorch

In linear regression, making a prediction means using the formula:

\begin{matrix} y = w x + b \end{matrix}

But for the model to be useful, we need to find the best values for w (slope) and b (bias) — the ones that make the fitted line pass through (or at least come close to) most of the data points, like in the fuel consumption chart above. This line represents the general relationship between x and y. When fitted correctly, it allows our predictions to be as close as possible to the actual values.

In this example, we’ll start with some initial guesses for w and b, since we don’t know their true values yet. The process of training the model is essentially about updating these values repeatedly until we find the best-fitting line.

We’ll use PyTorch to perform what’s called a forward pass — this simply means plugging in the guessed values of w and b to generate a prediction.

import torch  # Import the PyTorch library

# Initialize slope (w) and bias (b) with some starting values
# 'requires_grad=True' lets PyTorch track changes for training later
w = torch.tensor(2.0, requires_grad=True)
b = torch.tensor(-1.0, requires_grad=True)

# Define the prediction function (also called the forward pass)
# It uses the equation y = wx + b
def forward(x):
    return w * x + b

# Create a tensor input value: electricity usage = 3 units
x_input = torch.tensor([[3.0]])

# Call the forward function to get the predicted bill (ŷ)
y_pred = forward(x_input)

# Print the prediction as a regular number (not a tensor object)
print("Predicted electricity bill:", y_pred.item())

Let’s look at the output: Predicted electricity bill: 5.0

Here’s how it was calculated using the formula

w = 2.0 (slope)
b = -1.0 (bias)
x = 3.0 (input value)

\begin{matrix} y = (2.0 \times 3.0) + (- 1.0) = 6.0 - 1.0 = 5.0 \end{matrix}

So the model predicts a bill of 5.0 units for 3 units of electricity usage using our initial guesses for w and b.

Of course, in a real scenario, these values may not match the actual bill — and that’s where loss and training come in.

4. Evaluating Predictions: Loss and Cost Functions

Now that we’ve made a prediction (the forward pass) using our guessed values of w and b, a question comes up:

How do we know if our prediction is good or bad?

Remember, we’re trying to find the correct values of w and b through trial and error. But how can we compare our guessed values to the true ones?

Great question!

Think back to the dots on the chart we saw earlier, showing the actual electricity bills (y values) against usage (x). That chart is basically a collection of real data points:
→ “For this usage (x), the bill was actually this much (y).”

So when we predict the bill for a certain usage using our model, we can compare our predicted value to the real value from the data — just like checking if our prediction is close to the correct value.

4.2 Here's how we evaluate how good or bad the prediction is:

✅Loss Function (One Prediction)

What is it?
A formula to measure how far off a single prediction is from the real value.
Why use it?
To quantify the difference between what the model guessed and what the data says.
How it’s calculated:

\begin{matrix} L o s s = (y_{a c t u a l} - y_{p r e d i c t e d})^{2} \end{matrix}

Why squared?
Squaring makes sure all differences are positive and penalizes large errors more than small ones.

✅ Cost Function (All Predictions)

What is it?
The average of all the loss values across the dataset.
Why use it?
To evaluate the model’s overall performance — not just on one point, but across all examples.
Formula:

\begin{matrix} C o s t (M S E) = \frac{1}{N} \sum_{i = 1}^{N} (y_{i} - {\hat{y}}_{i})^{2} \end{matrix}

MSE: Mean Squared Error — the cost (average error) over all predictions
N: Total number of data points (how many x–y pairs we have)
i: Index of the current data point in the dataset
yᵢ: Actual (true) value of the target for the i-th data point
ŷᵢ: Predicted value from the model for the same i-th data point
(yᵢ − ŷᵢ)²: Squared difference (error) between the actual and predicted values

What does it tell us?
- A high cost means our model is making poor predictions.
- A low cost means our model is doing well.
- Our goal: Find the values of w and b that make the cost as low as possible.

4.3 Let’s Evaluate Our Previous Prediction

Earlier, we used:

w = 2.0, b = -1.0
x = 3.0
The model predicted: ŷ = 5.0

Now let’s assume the actual electricity bill (y_actual) for that usage is 6.0.

Using the loss formula:

\begin{matrix} L o s s = (6.0 - 5.0)^{2} = 1.0 \end{matrix}

So the model’s prediction has a squared error of 1.0 — this is our feedback signal.

Next, we’ll see how to use that feedback to improve the prediction by adjusting w and b.
Let’s move on to Section 5: Gradient Descent.

5. Gradient Descent in Linear Regression with PyTorch

After evaluating our prediction, we saw that the loss was 1.0 — not bad, but definitely not perfect.
Our goal now is to adjust the values of w and b so that our predictions become more accurate and the loss gets smaller.

How much smaller?
Well, ideally the loss would be 0, but in real-world scenarios that’s rarely possible. If you look again at the chart with dots (actual data points), you’ll notice that there’s no single line that perfectly touches all the dots — and that’s okay! Our goal is to find the best possible line — one that minimizes the average error across all predictions.

To achieve this, we use a method called gradient descent. This technique is essential when training models in Linear Regression with PyTorch, especially when working with real data.

5.1 What is Gradient Descent?

Let’s break down the name:

“Gradient” refers to the slope or direction of change — and yes, it suggests we’re making gradual updates.
“Descent” means moving downward, like walking downhill toward a minimum value.

So gradient descent is a method that helps us gradually adjust w and b to find the lowest point on the loss curve — where predictions are most accurate.

🧠 Analogy:

Imagine you’re standing on a foggy hill (just like in the featured image from this post). Your goal is to reach the bottom — the point with the lowest possible loss.
You can’t see very far ahead, but you can feel the slope beneath your feet.
So what do you do?
You take small steps downhill, adjusting your path as you go — that’s exactly what gradient descent does.

5.2 How It Works

You make a small update to w and b (a step).
Then check: Did the loss get better or worse?
If the loss decreased, you’re moving in the right direction — so keep going!
If the loss increased, you’re going the wrong way — adjust.

This is repeated many times until we find the best values.

The gradient tells us the direction to move.
The learning rate controls how big each step is.
👉 You can think of it like the size of your footsteps.

5.3 PyTorch Implementation (Full Code Example)

Let’s bring everything together — using the same example as before:

Initial w = 2.0, b = -1.0
Input x = 3.0
Actual y = 6.0

import torch

# Step 1: Initialize parameters
w = torch.tensor(2.0, requires_grad=True)
b = torch.tensor(-1.0, requires_grad=True)

# Step 2: Define the forward pass
def forward(x):
    return w * x + b

# Step 3: Define input and actual target value
x_input = torch.tensor([[3.0]])
y_actual = torch.tensor([[6.0]])

# Step 4: Set learning rate
learning_rate = 0.01

# Step 5: Run gradient descent for 100 steps
for epoch in range(100):
    y_pred = forward(x_input)                     # Make prediction
    loss = (y_actual - y_pred).pow(2).mean()      # Mean squared error
    loss.backward()                               # Compute gradients

    with torch.no_grad():                         # Update parameters
        w -= learning_rate * w.grad
        b -= learning_rate * b.grad

    w.grad.zero_()                                # Reset gradients
    b.grad.zero_()

# Step 6: Show final values and prediction
print("Final w:", w.item())
print("Final b:", b.item())
print("Final prediction:", forward(x_input).item())

After running the code, you’ll see output like:

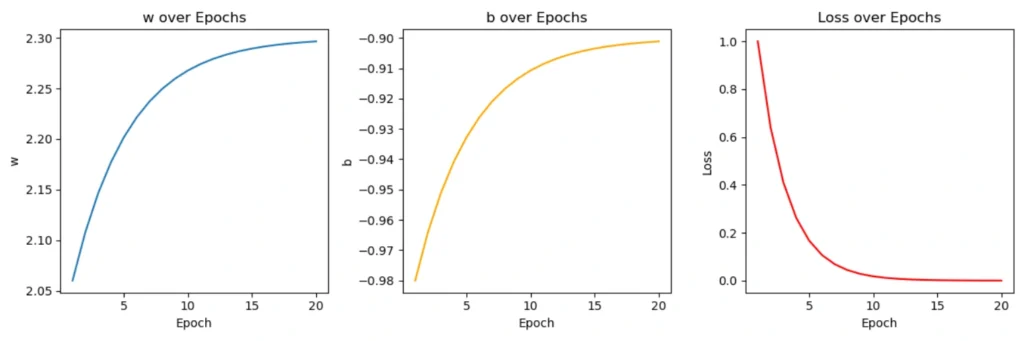
Final w: 2.299999475479126
Final b: -0.9000000953674316
Final prediction: 5.999998569488525

This means:

PyTorch found better values of w and b
Our final prediction is now very close to the actual value of 6.0
The loss is much smaller than when we started

The plot below shows how PyTorch gradually improves the values of w and b while reducing the loss step-by-step. This is how the model “learns” to make better predictions using gradient descent.

6. Real-World Considerations

So far, we’ve focused on the fundamentals — adjusting w and b for a single data point using manually written gradient descent. But in In real-world applications of Linear Regression with PyTorch, predictions often rely on multiple input variables, things get more complex.

For a deeper understanding of how these variables are represented and manipulated in PyTorch, consider reading our guide on Tensors in PyTorch.

To dive deeper into the math behind gradient descent, check out this excellent Stanford CS231n guide

Additionally, as you advance in machine learning, you’ll encounter various terminologies and concepts. Our AI & ML Glossary for Beginners can serve as a handy reference.

Here’s what you need to consider when moving beyond this simple example:

6.1 More Than One Input Variable

In real scenarios, predictions are rarely based on just one input like electricity usage.
You might need to predict based on multiple features, like usage, location, time of year, and more.

➡️ This turns simple linear regression into multiple linear regression, where you have:

\begin{matrix} y = w_{1} x_{1} + w_{2} x_{2} + \dots + w_{n} ​ x_{n} + b \end{matrix}

6.2 Using Built-in Optimizers

In this post, we manually updated w and b using .backward() and .grad. While this is great for learning, PyTorch offers built-in optimizers like:

torch.optim.SGD (Stochastic Gradient Descent)
torch.optim.Adam (Adaptive Moment Estimation)

These make training faster, more efficient, and easier to scale.

6.3 Validating with More Data

We used just one point (x = 3, y = 6) to illustrate how the model learns.
In practice, you train your model on a dataset, and you also need to validate it to make sure it works well on new data it hasn’t seen before.

This is called generalization, and it’s critical to avoid a model that only memorizes data instead of learning patterns.

7. Summary: What You’ve Learned About Linear Regression with PyTorch

Let’s quickly recap what you’ve learned in this guide:

✅ The basics of Linear Regression with PyTorch
✅ How to use PyTorch for making predictions
✅ What loss and cost functions are — and why they matter
✅ How gradient descent helps optimize your model
✅ How to train both slope and bias together to make accurate predictions
✅ And what to consider when taking your skills into real-world projects

✍️ What to Write (Copy-Paste Ready):

🔗 Get the Full Code on GitHub
You can access the complete, well-commented Python code used in this tutorial here:
👉 View Full Code on GitHub
It includes:
Manual gradient descent using PyTorch
Forward pass, loss calculation, and parameter updates
Plots showing how the model improves over time
Matching all steps discussed in this post

💬 Your Feedback Matters!

I’d love to hear from you:

What part of this tutorial helped the most?
Was anything confusing or challenging?
Have you tried tools like TensorFlow or Scikit-learn before?
Want help applying linear regression to your own dataset?

👉 Head over to the Contact Page and send me a message!